機械システム工学科　教員・研究室：大月英明

「難しさ」＝「コンピュータの計算時間」

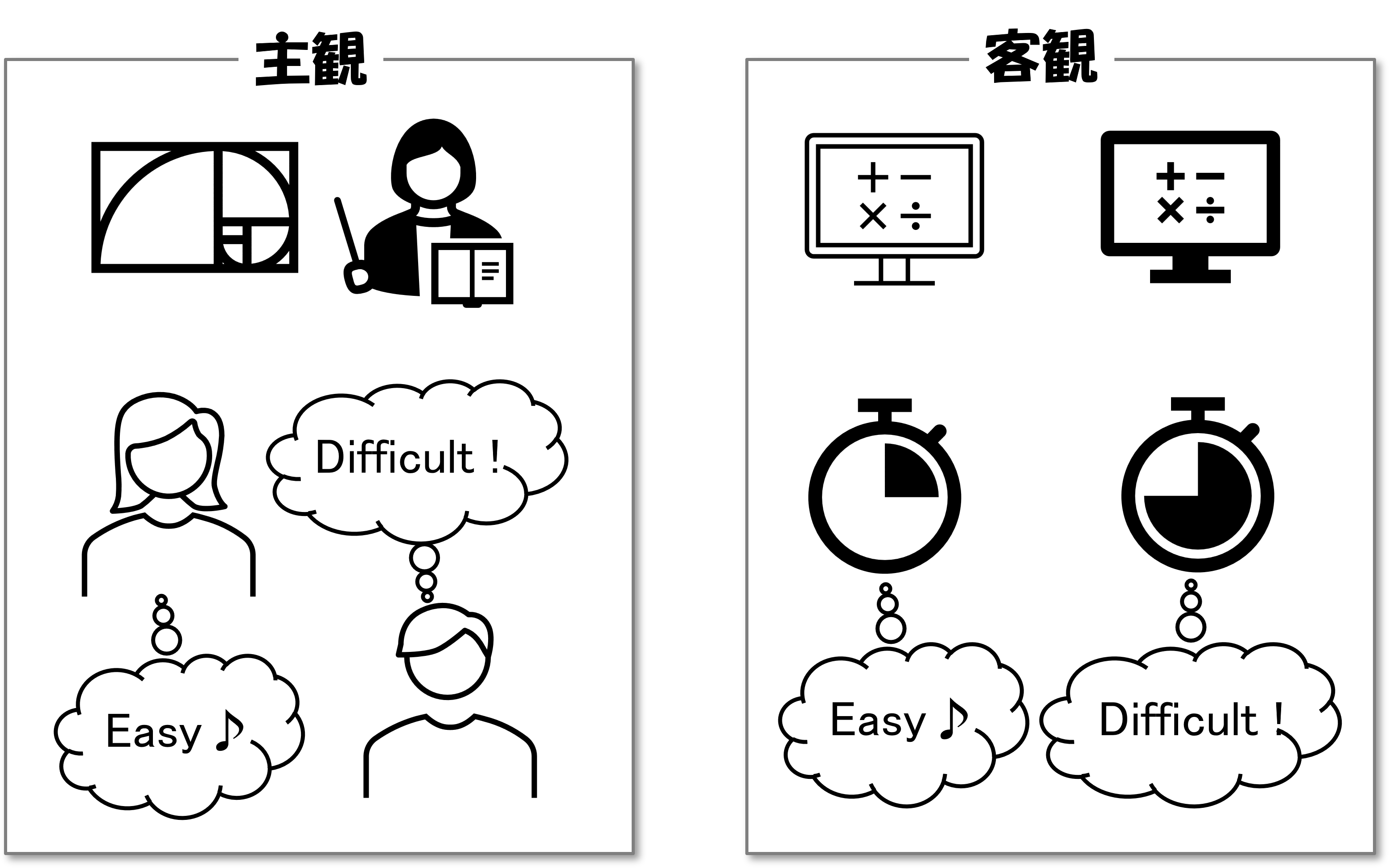
大学入試だと「○○大学の問題は難しい」とか「××大学の問題は簡単だ」と思う事があるでしょう。しかし、この「難しい」という言葉はとても主観的なもので、ある人にとっては難しいけれど、別の人にとっては簡単、というのはよくある事です。そこで誰もが納得する客観的な「問題の難しさ」を決めるために、研究者たちは「問題を解くために必要な計算ステップ数」という基準を用意しました。簡単に言うと、コンピュータが問題を解くために必要な「計算時間」を「問題の難しさ」と定義した、ということになります。

難しさの「度合い」

この基準を使って様々な問題を調べると、上手にプログラム（アルゴリズム）を作る事によって、家庭のパソコンでも割と早く解ける「朝飯前」な問題や、反対にスーパーコンピュータを使っても「宇宙の年齢以上の時間をかけないと解けない」ような問題など、問題の難しさにはっきりとした区別があることがわかってきました。簡単な問題は「クラスP」、難しい問題は「NP困難」と呼ばれています。

「完璧な答え」ではなく「それなりの答え」

問題の「完璧な答え（厳密解）」が求まることが一番うれしいわけですが、NP困難な問題、クラスPでも規模が大きすぎる問題では、計算時間が膨大となり現実的ではありません。そこで代わりに「それなりの答え（近似解）」を求める方法が開発されています。良い「それなりの答え」が求まれば、「完璧な答え」に迫ることができますし、「それなりの答え」で十分な場合も多くあります。

「それなりの答え」を効率的に解く方法とは？

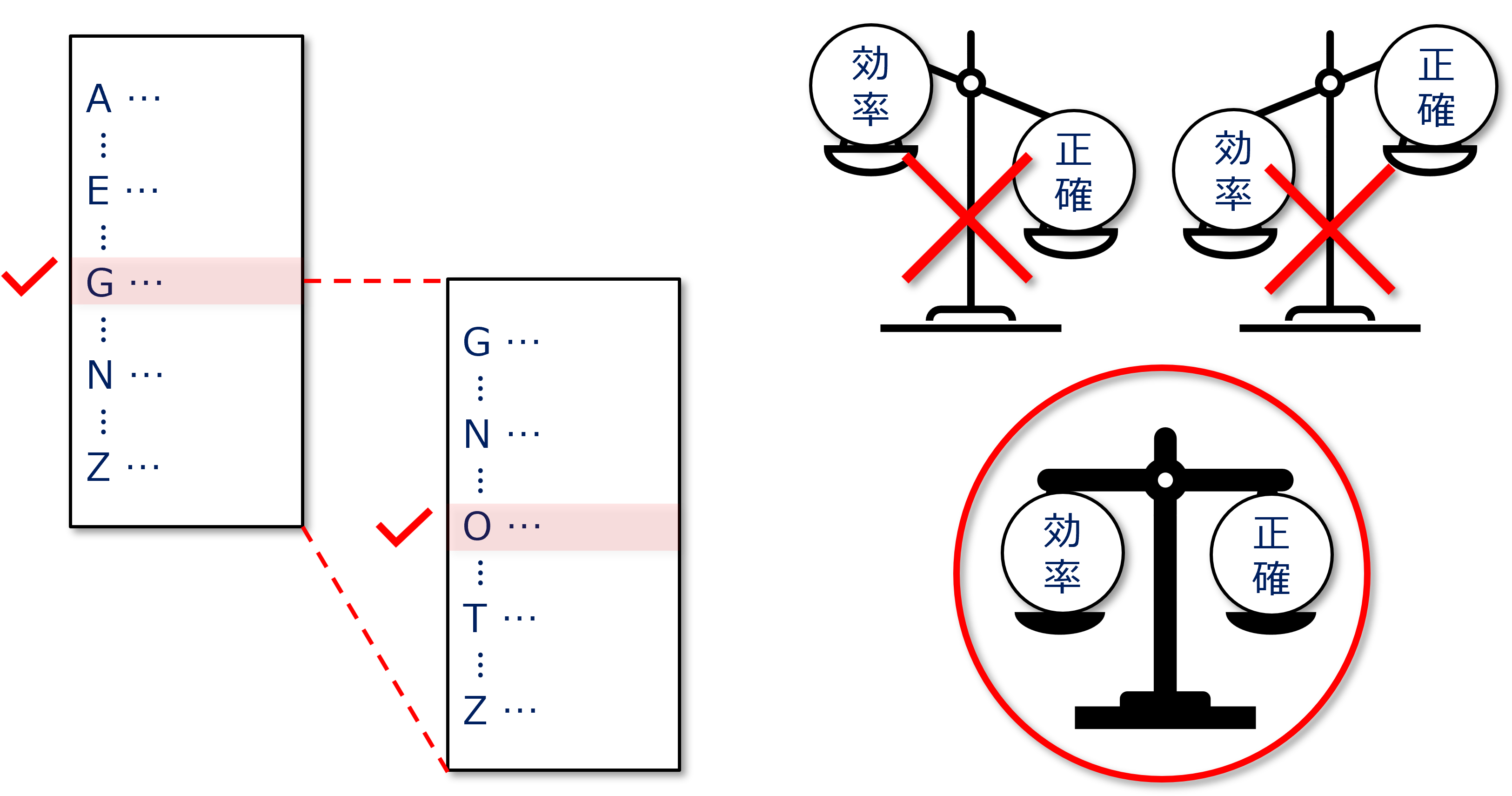
コンピュータで問題を解く場合、トライ＆エラーを繰り返して答えに段々と近づいて行きますが、闇雲にやっていては計算が終わりません。そのため、早い時間で計算できる「効率的な方法(アルゴリズム)」を開発する必要があります。例えば、名簿から Otuski を見つける問題の場合、先頭から順に調べる人は誰もいないでしょう。名簿のデータの真ん中をチェックすれば、Otsuki が「真ん中のデータの前か後ろか」分かるので、半分のデータは調べる必要がありません。引き続いて、残った半分のデータの真ん中を再度チェックすれば，またデータは半分になります。このような解法は二分探索と呼ばれるもので、他にも色々な効率の良い方法があります。

「どの程度」それなりが良いのか？

「それなり答え」は、できるだけ「完璧な答え」に近い方が良いのは当然です。しかし、ほとんど簡単化せず「正確さ」を優先させた場合、計算速度は低下して使い物になりません。逆に計算の「効率さ」を優先させ過ぎると、「正確さ」はまったく無くなってしまいます。この、早く効率的に計算できる、それなりの答えの「簡単化の限界」を明らかにすることが大変重要であり、研究のゴール・方向性を決めることになります。

主な研究業績

• "A New Polynomial-Time Solvable Graph Class for the Minimum Biclique Edge Cover Problem", IEICE TRANSACTIONS on Discrete Mathematics and Its Applications, Vol.E103-A,No.10 (2020)