例えば地球の形を考慮した
統計解析手法を探る
データを集めてグラフに表すと、特徴的な構造が表れることがあります。例えば、地球上を移動する複数の台風の進路データは、球面上に並べることができます。渡り鳥や魚が移動する軌跡なども、同じく球面上に並びます。球面上のデータ以外では、ある地点での年間の雷発生数は、1年を表す円周の上にプロットできます。従来の統計学では、どんなデータも果てのない平面上で扱い、y=ax+bのグラフで表せるようなシンプルな統計モデルを使って分析してきました。しかし球体や円には、1周すれば元に戻る「周期性」があります。私はそのような周期性のある、球体や円、トーラス(ドーナツ型)、シリンダー(円筒)の構造を持つデータの統計解析手法、つまり「道具」を作る研究をしています。
球面や円周上では、位置を表すのに角度を使いますが、角度を扱う場合に従来の統計手法や確率モデルが通用しないことは、例えば23時と1時の平均が、(23+1)/2=12時ではなく0時であることから理解できるでしょう。新しい道具が必要なのはそのためです。そして新たな道具を使えば、データを自由に回転させ、任意の視点から分析できるようになります。平面の地図はどこを中心とするかで違う形になるのに対して、地球儀ならどの視点からも見られるのと同じです。この道具で台風の進路のビッグデータを解析すれば、従来の解析では分からなかった、新たな傾向が見えてくる可能性があります。
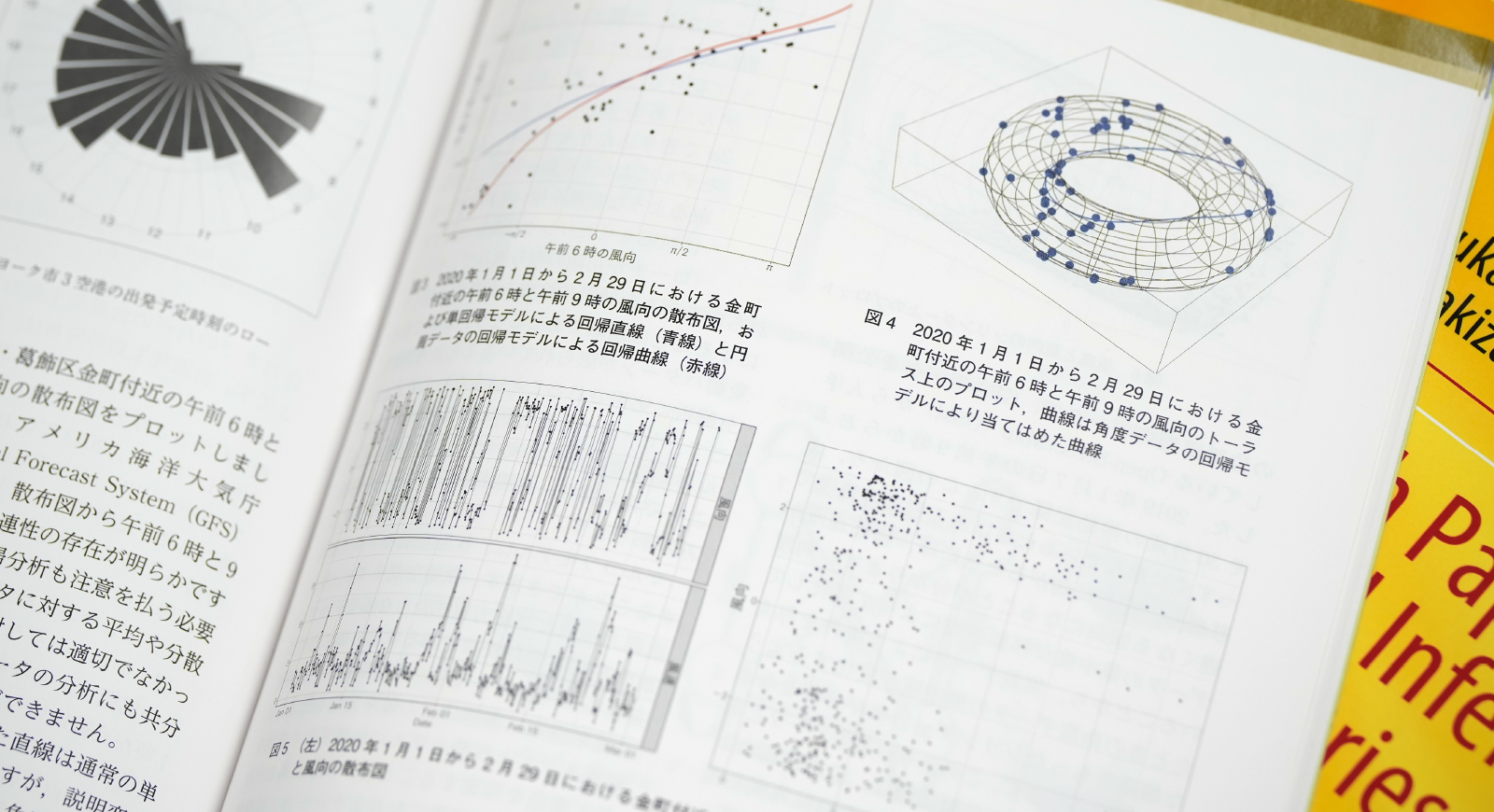
これまでの教科書の手法が使えない
構造上でのデータ解析を
あたりまえにしたい
進路選択はなんとなく理系へ進むものと思っていました。ところが、中学校時代に親しい友人たちから「文系か理系、どっちにする?」と聞かれたのがきっかけで視野が広がり、大学では経済学を専攻しました。そして、学ぶ中で統計学の時系列分析に興味を持ちました。大学院で学んだ「時系列のスペクトル解析」が形を持った統計学、いわゆる方向統計学と関連すると気付いたのは最近のことです。時系列のゆらぎ成分を表すスペクトル分布は、円周分布の密度関数と同じ構造なのです。このような「1周すると元に戻る構造のデータを解析・分析する」ことに興味をもっていて、それが現在の研究につながっています。
形を持つデータの統計解析は、昔から研究されてはいたものの、AIや機械学習、クラウドコンピューティングなどの計算技術が発達した近年になって、ようやく容易に統計分析できる環境が整いました。ただし、研究者コミュニティは世界各国を合わせてもそれほど大きいわけではなく、お互い誰が何をしているかを確認しながら交流できる規模です。多数の研究者がひしめくような世界ではなく、それでいて統計解析の教科書の新たな1分野になる可能性があり、注目を集め始めている分野だと感じられるところが魅力です。データサイエンスのさまざまな現場で広く役立つこの道具が、あたりまえの存在となることを目指して、研究に励んでいます。

「道具」を作るのが研究の目的
研究に時間を使う
楽しさを知ってほしい
角度データの統計学を含め、データサイエンスはどの分野にでも応用できる学問です。副専攻制がある南山大学では、そのような応用研究にも取り組めます。ソフトウェア工学と組み合わせれば、ITシステムやサービスのデータを収集して新サービスに活かす研究ができますし、すでに世の中ではそのようなサービスに、データサイエンスはあたりまえに使われています。機械システム工学科や電子情報工学科の学びと組み合わせれば、ロボットや機械の制御、通信ネットワークへの応用もできます。このように、どの分野にも関連するデータサイエンスの手法を、私の研究室では統計学を通じて身につけることができます。
研究というものは、飛び抜けて頭のいい人や才能がある人にしかできないものではありません。楽器を演奏しなくても音楽は楽しいし、スポーツやゲーム、囲碁や将棋も、うまい下手に関わらず楽しいと思えますよね。それぞれ個人の楽しみ方をすればいいのです。研究も同じように、才能に関係なく、やっていれば絶対に楽しいものです。自分で一つひとつ理解して腑に落ちる体験や、「このことは自分しか知らないだろうな」と思えるような、ワクワクする発見ができます。挑戦する前からあきらめてしまわずに、研究に時間を使うことの喜びや楽しさを、ぜひ大学で味わってほしいと思います。

Profile
データサイエンス学科 教授塩濱 敬之
専攻分野/統計科学



